Loïc Adam's PhD thesis "Learning Preferences under Severe Uncertainty"

Posted on May 9, 2024 by Loïc Adam (edited by Arthur Van Camp)
[ go back to blog ]

I defended my PhD thesis “Apprentissage de préférences sous incertitude sévère” (“Learning Preferences under Severe Uncertainty” in English) the 23rd October 2023. I worked for 3 years at the laboratory Heudiasyc (Heuristic and Diagnostic of Complex Systems, UMR-CNRS 7253) of the Université de Technologie de Compiègne, France, under the supervision of Sébastien Destercke. My PhD committee included Hélène Fargier, Wassila Ouerdane, Nadjet Bourdache, prof. Frédéric Koriche, prof. Sylvain Lagrue and Olivier Spanjaard. Although my PhD manuscript is in French, my work can be found in English: Possibilistic preference elicitation by minimax regret and Handling inconsistency in (numerical) preferences using possibility theory.

Introduction

Multiple-criteria decision analysis (MCDA) is a branch of operational research concerned with the evaluation of several alternatives, each with several criteria, by an analyst whose aim is to help a decision-maker to make a decision among these alternatives. A criterion is a characteristic of an alternative on which the decision-maker bases a decision, for example, the price of a car or its speed. The difficulty of these problems stems from the fact that the criteria are generally conflicting: increasing the gain of one criterion often decreases the gain of other criteria. For example, a cheaper car is often less efficient. The decision-maker therefore typically has to make trade-offs between different criteria, and the analyst has to help them determine which trade-offs are the most appropriate. Multi-criteria decision analysis therefore draws on a number of disciplines, including mathematics, computer science, philosophy, economics and sociology, to understand how a decision-maker makes a decision, and thus determine the best strategy to assist them. This branch of research is fairly recent, with the first works dating back to the 1960–1970s [1, 2, 3].

To help the decision-maker, it’s imperative to determine their preferences, to understand which criteria and trade-offs they favour. Asking the decision-maker directly how they judge an alternative seems complicated and therefore illusory. Common practice tells to elicit the decision-maker’s preferences, i.e. to formulate them so that they can be exploited. To do this, the analyst focuses on a family of preference models for the decision-maker, and through a series of questions, the analyst determines which preference model best matches the decision-maker’s preferences, which is then used to determine which decision to take from the available alternatives. There are a number of models that represent the attractiveness of a multi-criteria alternative, such as the weighted average, the ordered weighted sum (OWA) [4] or the Choquet integral [5], the latter allowing complex interactions between criteria.

The advantage of multi-criteria decision analysis is that it can be applied to a wide range of situations. It is thus possible to design recommendation and decision-making tools in different contexts, for example to judge different candidates for a job, manage budgets, recommend products… Nevertheless, in more critical contexts, such as in the medical or military fields, it seems essential to guarantee that the recommendation is robust to small changes, as the information on the decision-maker’s preferences may be uncertain (for instance due to lack of focus, alternatives that are too similar or distant…). The management of uncertainty is an increasingly studied issue, notably with the emergence of imprecise probabilities, which offer different frameworks for representing and dealing with uncertainty. By handling uncertainty correctly, it is possible to detect inconsistency, and therefore to analyse and correct it, thus improving the elicitation process, particularly if the initial problem is poorly modelled or the decision-maker is unreliable.

Contributions

A standard approach in the state of the art, robust incremental elicitation [6, 7], minimises cognitive cost (minimising the number of questions for the user) while offering strong performance guarantees. However, this approach cannot handle uncertain preferences (e.g., the user is not sure of what they prefer, or the aggregation function does not sufficiently model interactions between criteria). Current approaches that can do so, do not offer the same performance guarantees (only in terms of expectation) [8, 9, 10]. We therefore proposed an algorithm for eliciting uncertain preferences based on possibility theory [11, 12], a mathematical framework for modelling uncertainty. Our approach allows us to extend robust incremental elicitation (set approach) and obtain the same performance guarantees when there is no uncertainty, while being able to handle uncertain preferences. We can thus detect inconsistencies between preferential information, regardless of the source of the inconsistency, which is confirmed through synthetic experiments. The transition from set-based to possibilistic preferential information is shown in Figure 1. Note that, to obtain possibilistic information from the user’s answers, we ask the user (or the expert) for a confidence level \(\alpha\); that quantifies the uncertainty of the preference (from 0 to 1: 1 if they are fully certain, 0 if they cannot compare the alternatives).

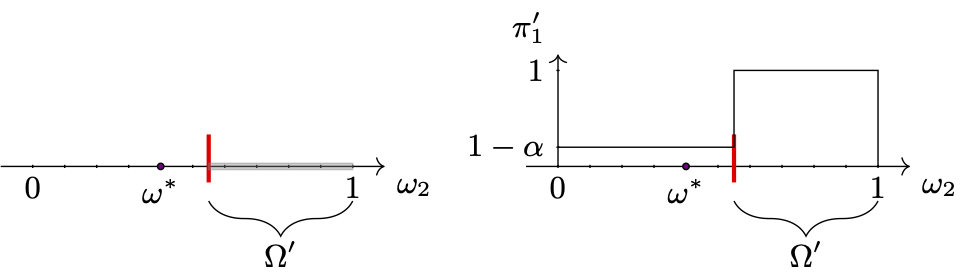
After proposing an approach for modelling uncertain preferences and detecting inconsistencies, we first proposed solutions for inferring despite this inconsistency. We then studied various information fusion operators [13] for handling uncertain preference information. These can restore consistency when the source of inconsistency comes from the user (wrong answers) and, ideally, improve the quality of recommendations. In addition to these proposals and the justification of their interest, we have carried out synthetic experiments. These show that inference strategies lead to higher-quality recommendations, while fusion operators provide information on which answers are wrong (or their minimum number). An example of the fusion of inconsistent possibilistic preferential information is shown in Figure 2, where we initially see that information \(S_3\) and \(S_4\) are inconsistent with each other (there is no \(\omega_1\) value such that \(\pi_{S_3}(\omega_1) = \pi_{S_4}(\omega_1) = 1\)), explaining why merging (via a conjunction) these different pieces of information does not result in coherent synthetic information. Nevertheless, thanks to two fusion operators based either on the choice of a maximal coherent subset (a subset of coherent answers that is as large as possible, i.e. \(\{1,2,3\}\) or \(\{1,2,4\}\)) [14] or on the assumption of \(\ell\) correct answers among \(k\) (we don’t specify which are the correct answers, just their number), it is possible to restore coherence (maximum of the possibility function, which is 1).

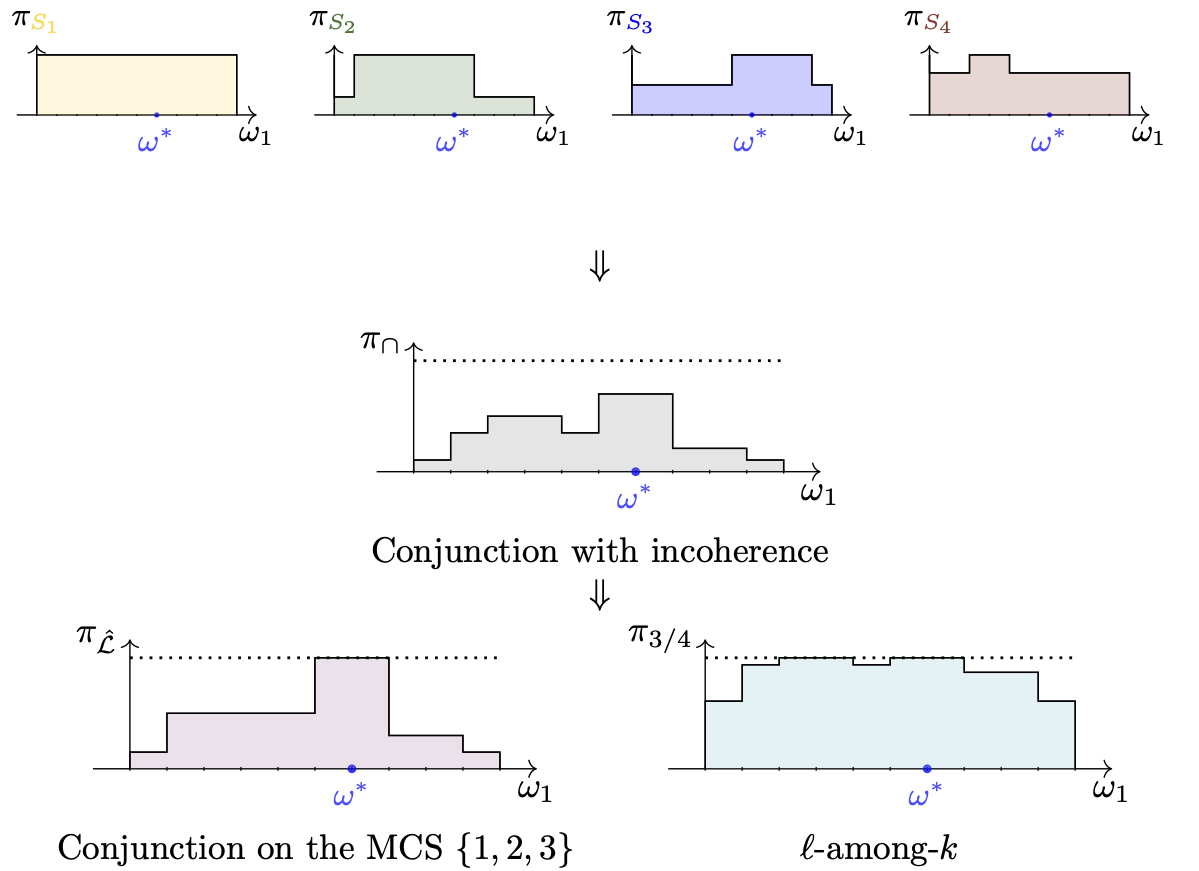
References

[1] Benayoun, R., De Montgolfier, J., Tergny, J. and Laritchev, O. Linear programming with multiple objective functions: Step method (stem), Mathematical programming, vol. 1, pp. 366–375, 1971. doi:10.1007/BF01584098

[2] Keeney, R. L. and Raiffa, H. R. Decisions with multiple objectives: preferences and value trade-offs, John Wiley & Sons, New York, 1976.

[3] Zionts, S. and Wallenius, J. An Interactive Programming Method for Solving the Multiple Criteria Problem, Management Science, vol. 22(6), pp: 652–663, 1976. doi:10.1287/mnsc.22.6.652

[4] Yager, R. R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking, IEEE Transactions on Systems, Man, and Cybernetics, vol. 18(1), pp: 183–190, 1988. doi:10.1109/21.87068

[5] Choquet, G. Théorie des capacités, Annales de l’Institut Fourier, vol. 5, pp: 131–295, 1954. doi:10.5802/aif.53

[6] Benabbou, N., Perny, P. and Viappiani, P. Incremental elicitation of choquet capacities for multicriteria choice, ranking and sorting problems, Artificial Intelligence, vol. 246, pp:: 152–180, 2017. doi:10.1016/j.artint.2017.02.001

[7] Bourdache, N. and Perny, P. Active preference learning based on generalized gini functions: Application to the multiagent knapsack problem, Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33(01), pp: 7741–7748, 2019. doi:10.1609/aaai.v33i01.33017741

[8] Brochu, E., Nando, F. and Abhijeet, G. Active Preference Learning with Discrete Choice Data, Advances in Neural Information Processing Systems, vol. 20, 2007 proceedings.neurips.cc/paper/2007/hash/b6a1085a27ab7bff7550f8a3bd017df8-Abstract.html

[9] Viappiani, P. and Boutilier, C. Optimal bayesian recommendation sets and myopically optimal choice query sets, Advances in Neural Information Processing Systems, vol. 23, 2010. papers.nips.cc/paper_files/paper/2010/hash/550a141f12de6341fba65b0ad0433500-Abstract.html

[10] Bourdache, N., Perny, P., and Spanjaard, O. Incremental Elicitation of Rank-Dependent Aggregation Functions based on Bayesian Linear Regression, Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, pp: 2023–2029, 2019. doi:10.24963/ijcai.2019/280

[11] Dubois, D. Belief structures, possibility theory and decomposable confidence measures on finite sets, Computers and Artificial Intelligence, vol. 5, pp: 403–416, 1986. 10.5555/16776.16779

[12] Dubois, D. and Prade, H. Possibility Theory, Probability Theory and Multiple-Valued Logics: A Clarification, Annals of Mathematics and Artificial Intelligence, vol. 32, pp: 35–66, 2001. doi:10.1023/A:1016740830286

[13] Dubois, D., Liu, W., Ma, J. and Prade, H. The basic principles of uncertain information fusion. An organised review of merging rules in different representation frameworks, Information Fusion, vol. 32 part A, pp: 12–39, 2016. doi:10.1016/j.inffus.2016.02.006

[14] Rescher, N. and Manor, R. On inference from inconsistent premisses, Theory and Decision, vol. 1, pp: 179–217, 1970. doi:10.1007/BF00154005

About the author

Loïc Adam is a former doctoral student at the laboratory Heudiasyc (Heuristic and Diagnostic of Complex Systems, UMR-CNRS 7253) of the Université de Technologie de Compiègne, France, where he worked under the supervision of CNRS Research Director Sébastien Destercke. His doctoral research focused on learning preferences under different types of severe uncertainty.