SIPTA
The Society for Imprecise Probabilities:
Theories and Applications

Andrea Wiencierz's PhD thesis on Regression analysis with imprecise data

Posted on April 24, 2014 by Andrea Wiencierz
[ go back to blog ]

My PhD thesis deals with the statistical problem of analyzing the relationship between a response variable and one or more explanatory variables when these quantities are only imprecisely observed. Regression methods are some of the most popular and commonly employed methods of statistical data analysis. Like most statistical tools, regression methods are usually based on the assumption that the analyzed data are precise and correct observations of the variables of interest. In statistical practice, however, often only incomplete or uncertain information about the data values is available. In many cases, the incomplete or uncertain information about the precise values of interest can be expressed by subsets of the observation space. For example, interval-censored and rounded data can be represented by intervals. As the representation by subsets allows considering many different forms of uncertainty about data within the same framework, this representation is adopted in my thesis and set-valued observations of real-valued variables are simply called imprecise data.

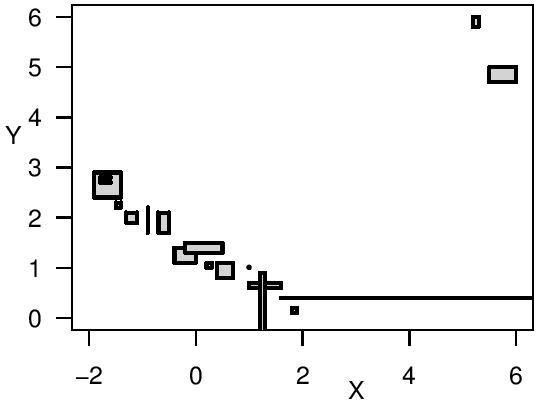
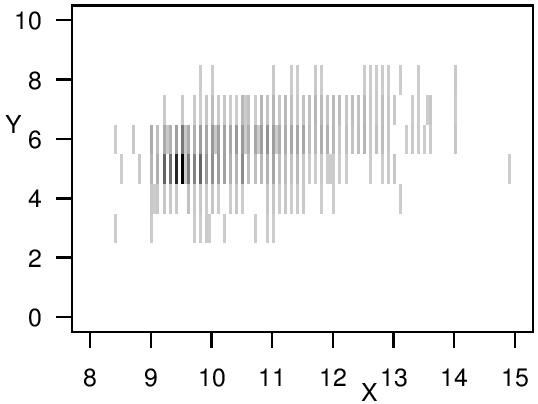
The aim of my PhD research was to find a regression method that provides reliable insights about the analyzed relationship, even if the variables are only imprecisely observed.

After a review of different approaches proposed in the literature, in my thesis, I present the likelihood-based approach to regression with imprecisely observed variables that we developed in Cattaneo and Wiencierz (2012) and that is named Likelihood-based Imprecise Regression (LIR). In the LIR framework, the regression problem is formalized as a decision problem whose actions are the possible regression functions, whose states are the considered probability distributions, and whose loss function is usually a characteristic of the residuals’ distribution. The LIR methodology consists in determining likelihood-based confidence regions for the loss of the regression problem on the basis of imprecise data and in regarding the set of all regression functions that are not strictly dominated as the imprecise result of the regression analysis. The confidence regions consist of the loss values associated with all probability measures that are (to a chosen degree) plausible in the light of the imprecise data, where the relative plausibility of the considered probability measures is measured by the likelihood function induced by the observations. Given the imprecise decision criteria, the Interval Dominance principle is applied to identify the set-valued result. Hence, a LIR analysis usually yields an imprecise result, which can be interpreted as a confidence set for the unknown regression function.

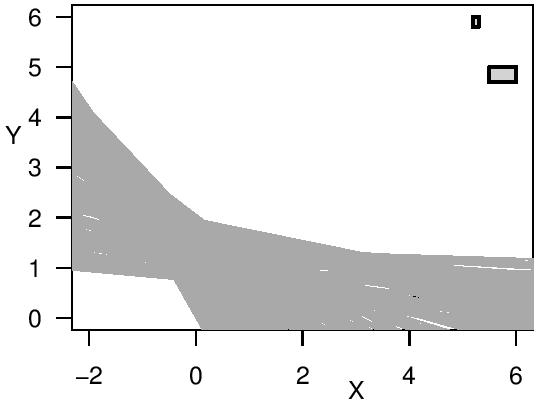
From the general LIR methodology, a robust regression method was derived in Cattaneo and Wiencierz (2012), where quantiles of the residuals’ distribution are considered as loss. Furthermore, an exact algorithm to implement this regression method for the special case of simple linear regression with interval data was developed in Cattaneo and Wiencierz (2013) and implemented in an R package (Wiencierz, 2012). In my thesis, I present and discuss these in detail. Moreover, I study several statistical properties of the robust LIR method. It turns out that this LIR method is robust in terms of a high breakdown point and that it yields highly reliable results in the sense that the coverage probability of the resulting set of regression functions seems to be generally rather high.

In addition to the robust LIR method, I also investigate an alternative approach that was proposed in Utkin and Coolen (2011). This approach generalizes Support Vector Regression (SVR) to situations where the response variable is imprecisely observed. It consists in applying a Minimin or a Minimax rule to the imprecise maximum likelihood estimates of the loss values associated with the regression functions, and in both cases yields a precise regression estimate. The set-valued decision criteria here consist of the loss values associated with all marginal probability distributions of the unobserved precise data that are compatible with the empirical distribution of the imprecise data. After discussing this approach in detail, I develop an alternative adaptation of SVR to this situation by following the LIR approach, which further generalizes these methods. In contrast to the Minimin and Minimax methods, the LIR method for SVR usually yields a set-valued result, which appears to be more appropriate when dealing with imprecise data. Moreover, the LIR framework has the advantage that it allows reflecting the data imprecision and accounting for statistical uncertainty at the same time, since both types of uncertainty are expressed by the extent of the set-valued result of the regression analysis.

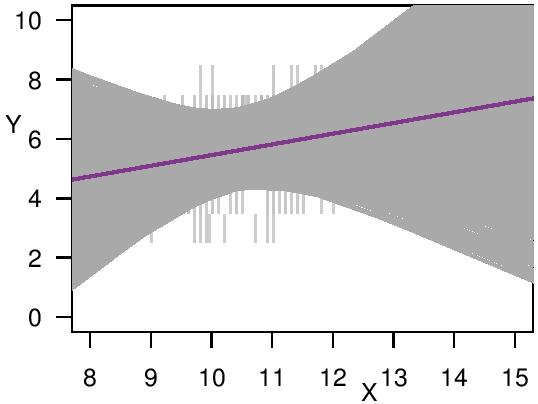
Finally, I apply the different regression methods to two practical data sets from the contexts of social sciences and winemaking, respectively. In both cases, the LIR analyses provide very cautious inferences.

References

About the author

Andrea Wiencierz works in the Working Group Methodological Foundations of Statistics and their Applications at the Department of Statistics of the LMU Munich, Germany, where she defended her PhD thesis on December 13, 2013.